Research Ideas and Outcomes : Research Article
Print
Research Article
A fast alignment-free bioinformatics procedure to infer accurate distance-based phylogenetic trees from genome assemblies
expand article info Alexis Criscuolo ‡
‡ Hub de Bioinformatique et Biostatistique – C3BI, Institut Pasteur, USR 3756, CNRS, Paris (75015), France, Metropolitan
Corresponding author: Alexis Criscuolo (alexis.criscuolo@pasteur.fr)
Received: 14 May 2019 | Published: 10 Jun 2019
© 2019 Alexis Criscuolo
This is an open access article distributed under the terms of the Creative Commons Attribution License (CC BY 4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Citation: Criscuolo A (2019) A fast alignment-free bioinformatics procedure to infer accurate distance-based phylogenetic trees from genome assemblies. Research Ideas and Outcomes 5: e36178. https://doi.org/10.3897/rio.5.e36178
Open Access

Abstract

This paper describes a novel alignment-free distance-based procedure for inferring phylogenetic trees from genome contig sequences using publicly available bioinformatics tools. For each pair of genomes, a dissimilarity measure is first computed and next transformed to obtain an estimation of the number of substitution events that have occurred during their evolution. These pairwise evolutionary distances are then used to infer a phylogenetic tree and assess a confidence support for each internal branch. Analyses of both simulated and real genome datasets show that this bioinformatics procedure allows accurate phylogenetic trees to be reconstructed with fast running times, especially when launched on multiple threads. Implemented in a publicly available script, named JolyTree, this procedure is a useful approach for quickly inferring species trees without the burden and potential biases of multiple sequence alignments.

Keywords

phylogenetics, alignment-free, genome, evolutionary distance, branch support, MinHash, Balanced Minimum Evolution, elementary quartets

Introduction

Evolutionary relationships between species are commonly represented by a phylogenetic tree inferred from multiple sequence alignments of orthologous genes. Tree reconstructions are generally performed from multiple gene datasets (e.g. core-gene set) because they enhance the overall phylogenetic signal by reducing the random error caused by a small number of characters (e.g. Hillis et al. 1994, Huelsenbeck 1995, Rokas et al. 2003, Criscuolo et al. 2006). Moreover, building large multiple gene datasets is facilitated by the increasing number of available genome sequences (Land et al. 2015). However, building a large number of orthologous sequence sets for phylogenomic purpose requires extensive genome mining and sequence processing steps that are time consuming, and often need manual interventions. In addition, long running times are also expected when inferring a phylogenetic tree from a large multiple gene dataset on hundreds of taxa.

To infer a phylogenetic tree that represents the evolutionary relationships of a set of genomes, an alternative approach is to estimate a pairwise distance between each pair of unaligned genomes, and to next build a phylogenetic tree with a fast distance-based reconstruction method. Such bioinformatics procedures are becoming popular because they allow dealing with thousands of assembled genomes, depend on few assumptions regarding their evolutionary process, and quickly lead to a phylogenetic tree with minimal manual intervention (Chan and Ragan 2013, Zielezinski et al. 2017). More formally, a distance-based alignment-free phylogenetic inference from genome sequences could be decomposed in four main steps.

The first step is the estimation of a dissimilarity value between each pair of unaligned genome nucleotide sequences. Many approaches were proposed to compute such values for a phylogenetic purpose, based on k-mer comparisons (e.g. Pride et al. 2003, Chapus et al. 2005, Wang et al. 2005, Sims et al. 2009, Yu et al. 2010, Sims and Kim 2011, Hatje and Kollmar 2012, Yi and Jin 2013, Chan et al. 2014, Leimeister et al. 2014, Ondov et al. 2016, Leimeister et al. 2017, Lees et al. 2018), common nucleotide substrings (e.g. Ulitsky et al. 2006, Domazet-Loso and Haubold 2009, Haubold et al. 2009, Yang et al. 2013, Horwege et al. 2014, Haubold et al. 2014), base distribution within genomes (e.g. Liu and Sun 2008, Yu et al. 2010, Deng et al. 2011, Gao and Luo 2011, Huang et al. 2011, Kolekar et al. 2012, Li et al. 2017), or local alignments (e.g. Henz et al. 2004, Auch et al. 2006, Deng et al. 2006, Deloger et al. 2008, Meier-Kolthoff et al. 2013, Yonezuka et al. 2017). Each of these methods have their own strengths and limitations, but many of them are not often used in practice because no current implementations exist or because they require quite important running times. 

The second step is the correction of each computed pairwise dissimilarity value into a numerical quantity that is proportional to the evolutionary distance between the corresponding genomes. An evolutionary distance is the number of substitution events per character that have occurred along the path separating two leaves within the 'true' phylogenetic tree representing the evolutionary relationships among genomes. This step is important because using pairwise dissimilarities that are non-linear with respect to evolutionary distances is expected to lead to incorrect phylogenetic tree topologies (Saitou and Imanishi 1989, Jin and Nei 1990, DeBry 1992, Rzhetsky and Sitnikova 1996, Susko et al. 2004, McTavish et al. 2015). Unfortunately, few alignment-free methods lead to genome dissimilarities that are explicitly corrected to approximate evolutionary distances (Domazet-Loso and Haubold 2009, Haubold et al. 2009, Haubold et al. 2014, Leimeister et al. 2017). 

The third step is the reconstruction of the phylogenetic tree from the estimated evolutionary distances. Many algorithms exist for this purpose (see e.g. Pardi and Gascuel 2016). Unfortunately, a lot of phylogenetic inference procedures from genome dissimilarities (e.g. Xu and Hao 2009, Cohen and Chor 2012, Yi and Jin 2013, Chan et al. 2014, Haubold et al. 2014, Leimeister et al. 2017, Li et al. 2017) are based on the average-linkage clustering (UPGMA; Sokal and Michener 1958) or Neighbor-Joining (NJ; Saitou and Nei 1987, Studier and Keppler 1988) algorithms, both being known to often lead to poor results (Bruno et al. 2000, Henz et al. 2004, Auch et al. 2006, Lees et al. 2018).

The final step is the estimation of a confidence value at each branch of the inferred tree. Several strategies were proposed to this aim (Pride et al. 2003, Chapus et al. 2005, Liu and Sun 2008, Haubold et al. 2009, Hatje and Kollmar 2012, Kolekar et al. 2012, Meier-Kolthoff et al. 2013, Yi and Jin 2013), but they are all based on resampling procedures (jackknife or bootstrap). They are therefore often neglected because requiring long running times.

This paper reports a new bioinformatics procedure that is based on well-argued choices for each of the four previously described steps. By analyzing simulated genome sequences, this procedure is shown to efficiently estimate the pairwise evolutionary distances between each pair of genomes, therefore allowing the reconstruction of accurate phylogenetic trees. This expected accuracy is illustrated by the analysis of 187 real genome datasets, representative of different genera within the bacterial, archaeal and eukaryotic phyla. All these analyses show that this novel bioinformatics procedure, implemented in the script JolyTree (gitlab.pasteur.fr/GIPhy/JolyTree), is an efficient approach to infer a phylogenetic tree from hundreds of genome assemblies in a few minutes.

Method and Implementation

To estimate a pairwise dissimilarity between each pair of genomes, the Mash method (Ondov et al. 2016) was chosen for two main reasons: its fast running time in practice and its close relationship with the p-distance (i.e. the proportion of observed nucleotide differences when comparing two aligned sequences). Given a chosen k-mer size and a sketch size \(s\), the Mash dissimilarity between two genome sequences \(i\) and \(j\) is determined by the following analytical formula:

 \( (1) ~~~~~~~~~~~~~~~~~~~~ m_{ij} = k^{-1} \Big( \log_e (1+J_{ksij}) - \log_e (2 \, J_{ksij}) \Big) \)

where \(J_{ksij}\) is an estimate of the Jaccard index between the two k-mer sets induced by \(i\) and \(j\) based on hashed k-mer subsets of size \(s\), called MinHash sketches (for more details, see Ondov et al. 2016). A MinHash sketch is quite fast to precompute from a genome assembly (e.g. few seconds from a prokaryote genome assembly, independently from the sketch size \(s\)), and the computation of \(J_{ksij}\) (and next \(m_{ij}\)) from a pair of MinHash sketches is nearly instantaneous in practice. Therefore, Mash is a method of choice to quickly estimate every pairwise distance from a large number of assembled genome sequences. Moreover, Ondov et al. (2016) observed that \(m_{ij} \approx a_{ij}\), where the dissimilarity \(a_{ij}\) is the one-complement of the Average Nucleotide Identity (ANI) between \(i\) and \(j\) (e.g. Deloger et al. 2008, Yonezuka et al. 2017). As \(a_{ij}\) is computed by averaging the proportion of nucleotide differences observed between every consecutive genome fragment (of size ~1Mb) from \(i\) against its best BLAST hit region within \(j\) (Goris et al. 2007), it could be seen as the average of the p-distances observed across consecutive homologous fragments from the genomes, therefore leading to \( a_{ij} \approx p_{ij}\) where \(p_{ij}\) is the expected p-distance between \(i\) and \(j\) (see e.g. Colston et al. 2014, Topaz et al. 2018). As pointed out by Ondov et al. (2016), the approximation \(m_{ij} \approx a_{ij}\) (\(\approx p_{ij}\)) mainly depends on a sufficiently large sketch size \(s\) (e.g. > 1,000), but also on a value of \(k\) that is large enough to minimize the probability \(q\) of observing a random k-mer shared by two genomes \(i\) and \(j\) by chance alone. Following Fofanov et al. (2004), they suggested to estimate \(k\) from the genome size \(g\) with the following formula:

 \((2) ~~~~~~~~~~~~~~~~~~~~ k = \lceil \log_4 \big( g \, (1-q) \big) - \log_4 \; q \rceil\).

Of note, when considering two genomes \(i\) and \(j\) of respective sizes \(g_i\) and \(g_j\), one can select \(g = \max ( g_i , g_j )\).

As the Mash dissimilarity \(m_{ij}\) approximates the expected p-distance \(p_{ij}\) that can be observed between the genome sequences \(i\) and \(j\), there exists several ways to correct the expected proportion of nucleotide differences into an estimated number of substitution events per character. Such corrections could be formalized by the following formula: 

 \((3) ~~~~~~~~~~~~~~~~~~~~ d_{ij} = -b_1 \log_e (1 - p_{ij} / b_2 ) \)

where \(b_1\) and \(b_2\) are defined according to explicit models of nucleotide sequence evolution. If equal nucleotide frequencies are observed and the rate of substitution is considered identical for all pairs of nucleotides, the correction formula \((3)\) is determined by \(b_1 = b_2 = 0.75\) (Jukes and Cantor 1969, Kimura and Ohta 1972) or by \(b_1 = b_2 = 0.75(1 - \phi)\) where \(\phi\) is the expected proportion of characters that are invariant with respect to indels and substitutions (McTavish et al. 2015). If the frequency \(\pi_x\) of each nucleotide \(x = \text{A}, \text{C}, \text{G}, \text{T}\) is expected to deviate from 0.25, an evolutionary distance can be estimated with \(b_1 = b_2 = 1 - \pi_\text{A}^2 - \pi_\text{C}^2 - \pi_\text{G}^2 - \pi_\text{T}^2 \) (Tajima and Nei 1982, Tajima and Nei 1984). This last estimate is based on the equal-input model of sequence evolution (F81; Felsenstein 1981), which assumes that the substitution rate is proportional to the frequency of the target nucleotide. However, if \( i\) and \(j\) arose from heterogeneous substitution patterns, an evolutionary distance based on the F81 model can be estimated by formula \((3)\) with \(b_1 = 1 - \pi_\text{A}^2 - \pi_\text{C}^2 - \pi_\text{G}^2 - \pi_\text{T}^2 \) and \(b_2 = 1 - \pi_{\text{A}_i} \pi_{\text{A}_j} - \pi_{\text{C}_i} \pi_{\text{C}_j} - \pi_{\text{G}_i} \pi_{\text{G}_j} - \pi_{\text{T}_i} \pi_{\text{T}_j}\), where \(\pi_{x_i}\) and \(\pi_{x_j}\) are the frequencies of the nucleotide \(x\) in sequences \(i\) and \(j\), respectively (Tamura and Kumar 2002). Knowing that two genomes are often expected to diverge following complex non-homogeneous and non-stationary evolutionary processes, this last evolutionary distance estimate was chosen to correct the p-distance approximated by the formula \((1)\), with nucleotide frequencies directly computed from the genome sequences \(i\) and \(j\).

The program FastME was chosen to perform the phylogenetic tree inference because it allows inferring accurate phylogenetic trees with very fast running times (Desper and Gascuel 2002, Desper and Gascuel 2003, Huang et al. 2011, Lefort et al. 2015). The Balanced Minimum-Evolution (BME) was selected as the criterion to optimize from the evolutionary distances \(d_{ij}\). The BME criterion considers as optimal the tree \(T\) with the smallest estimation \(\ell(T)\) of the tree length (for more details, see Pauplin 2000, Desper and Gascuel 2002, Desper and Gascuel 2003, Pardi and Gascuel 2016). Of note, BME is the tree optimality criterion of the greedy algorithm NJ (Gascuel and Steel 2006), but the tree inference implemented by FastME is based on an extensive hill-climbing method: starting from an initial tree, FastME explores the tree space using tree swapping approaches in order to find the BME phylogenetic tree. However, as the FastME program allows observing very fast running times, it has been used here to implement a more thorough phylogenetic tree search based on a data noising strategy (Charon and Hudry 1993, Morrison 2007, Criscuolo 2011) to avoid local optima. First, a hill-climbing tree search is performed by FastME to infer a BME tree \(T\) from the evolutionary distances \(d_{ij}\). Next, the following procedure is performed: (i) each evolutionary distance \(d_{ij}\) is replaced by a random value \(d^*_{ij} \in \big[ (1-\epsilon)d_{ij} , (1+\epsilon)d_{ij} \big]\) with a fixed \(\epsilon \in \, ]0, 1[\); (ii) a tree search is performed with starting tree \(T\) to infer a BME tree \(T^*\) from the noised distances \(d^*_{ij}\), followed by another tree search with starting tree \(T^*\) to infer a tree \(T'\) from the initial distances \(d_{ij}\); and (iii) the tree \(T\) is replaced by \(T'\) if \(\ell(T') < \ell(T)\). By repeating this procedure with different values \(\epsilon \in \, ]0, 1[\), this simple distance noising strategy increases the probability of reaching the BME global optimum within the tree space.

Finally, the program REQ (gitlab.pasteur.fr/GIPhy/REQ) was chosen for assessing the branch confidence values of the inferred tree. This tool estimates the rate of elementary quartets (REQ) for each branch of a given phylogenetic tree from the associated distances \(d_{ij}\), as described by Guénoche and Garreta (2001). This method simply computes the proportion of four-leaf subtrees (i.e. quartets) induced by every internal branch that are supported by the four-point condition applied to the six corresponding pairwise evolutionary distances (Zaretskii 1965, Buneman 1971). Therefore, this measure is not based on a random sampling (such as bootstrap-based confidence supports). The closer this measure is to 1, the more the corresponding branch is fully supported by the pairwise evolutionary distances \(d_{ij}\). Of note, REQ running time is quite fast (e.g. ~5 seconds with \(n\) = 500 on a standard computer).

The procedure described above was implemented in Bash (www.gnu.org/software/bash), therefore running on UNIX, Linux and most OS X operating systems. This implementation, named JolyTree, is freely available at gitlab.pasteur.fr/GIPhy/JolyTree. It directly reads a set of \(n\) assembled genomes in FASTA format from a specified directory. JolyTree allows setting the value of \(q\) (= 0.00001 by default) to estimate the k-mer size with formula \((2)\) from the size \(g\) of the largest genome. A unique sketch size \(s\) is defined as 25% of the average of the \(n\) genome lengths. As the computation of each pairwise Mash dissimilarity could be performed independently of the other ones, JolyTree allows this costly \(O(n^2)\) step to be executed on multiple threads. By default, all Mash dissimilarity values are automatically corrected by formula \((3)\) when at least one of them is larger than 0.1 (see below); however, this cutoff can be modified with dedicated option. The distance noising procedure is repeated 100 times by default with \(\epsilon\) varying from 0.1 (moderate noising) to 0.7 (important noising). All arithmetic operations are performed by gawk v. 4.1.4 (ftp.gnu.org/gnu/gawk). The results presented below were obtained using Mash v. 2.1 (github.com/marbl/Mash), FastME v. 2.1.5.1 (gite.lirmm.fr/atgc/FastME), and REQ v. 1.2 (gitlab.pasteur.fr/GIPhy/REQ).

Results and Discussion

Several analyses from simulated and real datasets were performed to show that JolyTree allows accurate phylogenetic trees to be quickly inferred from genome sequences. The following results illustrate the accuracy and treelikeness of the F81-corrected distance estimates, the usefulness of the data noising strategy for inferring trees, and the fast running times observed when analyzing large genome datasets. Some phylogenetic analyses of real-case genome datasets are also presented and discussed.

Simulation results

In order to observe the ability of JolyTree to estimate the evolutionary distance between a pair of genomes, a large number of sequence pairs was simulated. Given an evolutionary distance \(d\) varying from 0.05 to 0.60 (step = 0.05), the program SeqGen v. 1.3.4 (Rambaut and Grassly 1997) was used to simulate the evolution of 500 sequence pairs with \(d\) substitution events per character. For each simulated sequence pair, their length was randomly drawn from 1 million of bases (Mbs) to 10 Mbs, and their GC content from 25% to 75%. Each sequence pair evolution was simulated under the general time reversible model of nucleotide evolution (GTR; e.g. Yang 1994) with each of the six different rate parameters randomly drawn from ]0, 5[, and the \(\Gamma\)-distributed character-specific rate heterogeneity (Yang 1993) shaped by a parameter \(\alpha\) randomly drawn from 1 to 5. Finally, deletions were included within each simulated sequence with a probability of 0.012\(\, d\) (therefore varying from 0.06% to 0.72% depending on how large \(d\) is) at every character, with each indel length randomly drawn from 1 to 100. For each sequence \(i\) and \(j\), the Mash distance was computed with the k-mer size determined by formula \((2)\) with \(q\) = 0.00001, and the sketch size \(s\) defined as 25% of the sequence length average. Each computed distance was transformed into an evolutionary distance estimate with the F81 version of formula \((3)\) proposed by Tamura and Kumar (2002), as implemented by JolyTree. For each evolutionary distance \(d\), the obtained results are represented in Fig. 1.

a
b
Figure 1.

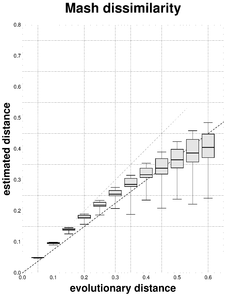
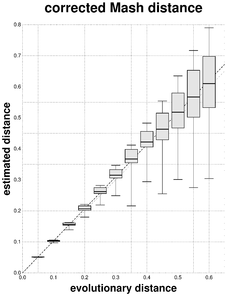
Box plots representing the mean, lower and upper quartiles, and 25th and 975th permilles of \(N\) = 500 estimates \(\hat{d}\) of the evolutionary distances \(d\) = 0.05, 0.10, ..., 0.60. Each linear regression through the origin with slope value b is represented with dashed lines.

a: Results obtained with the Mash dissimilarity; slope b = 0.7491, coefficient of determination of all points R2 = 0.9767, coefficient of determination of the 12 mean points R2 = 0.9917.  
b: Results obtained with the F81-corrected Mash distance; slope b = 1.0338, coefficient of determination of all points R2 = 0.9736, coefficient of determination of the 12 mean points R2 = 0.9998.  

As expected (e.g. Jin and Nei 1990, Nei and Kumar 2000, Tamura and Kumar 2002, Collins et al. 2012), both Mash dissimilarity and its F81 correction are quite good estimates of the 'true' evolutionary distance \(d\) when \(d\) < 0.1, with small standard error of the estimate (SEE) values (e.g. < 0.005; Fig. 2a, b). However, the Mash dissimilarity values are clearly non-linear with respect to \(d\), especially for large values of \(d\) (e.g. > 0.2; see Fig. 1a). As the Mash dissimilarity seems to induce a concave function of \(d\) (Fig. 1a and Fig. 2e), phylogenetic analyses based on dissimilarities computed by Mash could lead to incorrect trees (Susko et al. 2004). Surprisingly, F81-corrected distances obtained with formula \((3)\) are quite linear with respect to \(d\) (Fig. 1b and Fig. 2f), despite the fact that the associated equal-input model of nucleotide evolution is underparametrized in comparison with the GTR+\(\Gamma\) evolutionary model used for sequence simulation. Moreover, the F81 distance estimates are close to the 'true' evolutionary distances \(d\) on average, with SEE always smaller than the one observed with Mash (Fig. 2a, b) and slope values of the linear regression through the origin always very close to 1 for every value of \(d\) (Fig. 2f). Using Mash followed by a F81 correction therefore represents an accurate approach for phylogenetic inference. However, the linear residual standard deviation (RSD) plots show that the variance of the estimates rapidly grows with \(d\) (Fig. 2c, d), especially when using the F81 correction (Fig. 2d). Therefore, datasets inducing large values of \(d\) (e.g. > 0.4) could increase the possibility of inferring incorrect distance-based phylogenetic trees, or trees with inconvenient negative external branches caused by the violation of the triangle inequality (Desper and Gascuel 2003). Of note, k-mer sizes returned by formula \((2)\) with \(q\) < 0.00001 have led to smaller SEE and RSD but at the cost of slightly non-linear relationships between the F81-corrected distance estimates and \(d\), whereas \(q\) > 0.00001 allowed observing slope values that are slightly higher than 1 with very large SEE and RSD (not shown). No significant improvements were observed by increasing the sketch sizes \(s\) (not shown).

a
b
c
d
e
f
Figure 2.

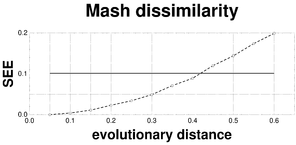
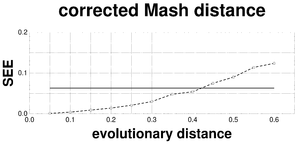
Plots associated to the data represented in Fig. 1. For each evolutionary distance \(d\) = 0.05, 0.10, ..., 0.60, standard error of the estimate (SEE) plots (Fig. 2a, b) represent the deviation of the estimates \(\hat{d}\), i.e. SEE = \(\sqrt{ \sum(d - \hat{d})^2/(N-2) }\). For each evolutionary distance \(d\) = 0.05, 0.10, ..., 0.60, linear residual standard deviation (RSD) plots (Fig. 2c, d) represent the deviation of the estimates \(\hat{d}\) from the overall linear fit \(bd\) (dashed lines in Fig. 1), i.e. RSD = \(\sqrt{ \sum(b d - \hat{d})^2/(N-2) }\). For each evolutionary distance \(d\) = 0.05, 0.10, ..., 0.60, linear slope plots (Fig. 2e, f) represent the slope value of the linear regression through the origin estimated from the estimates \(\hat{d}\). Each horizontal line represents the reference value (SEE: Fig. 2a, b; RSD: Fig. 2c, d; slope: Fig. 2e, f) estimated from all the data.

a: SEE plot of the Mash dissimilarity; reference SEE = 0.1017.   
b: SEE plot of the F81-corrected Mash distance; reference SEE = 0.0638.  
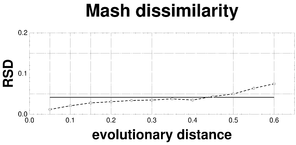
c: RSD plot of the Mash dissimilarity; reference RSD = 0.0426.  
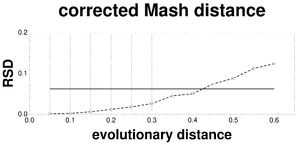
d: RSD plot of the F81-corrected Mash distance; reference RSD = 0.0626.  
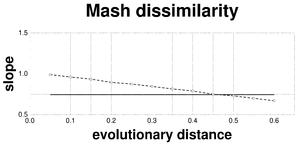
e: Linear slope plot of the Mash dissimilarity; reference slope = 0.7491.   
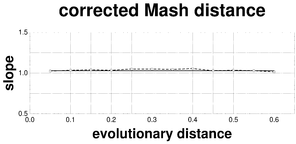
f: Linear slope plot of the F81-corrected Mash distance; reference slope = 1.0338.   

As JolyTree is expected to accurately estimate the evolutionary distance \(d\) between every pair of genomes that are not too distant (e.g. \(d\) < 0.5), this bioinformatics procedure is recommended for quickly inferring phylogenetic trees from genomes belonging to the same genus. It was used to reconstruct a phylogenetic tree from the \(n\) = 96 Listeria genome contig sets generated by Lees et al. (2018) from a representative model tree inferred by Kremer et al. (2016) from 2,177 core genes (Fig. 3a). These assembled genome contig sequences were obtained via a realistic simulation procedure, including GTR-based nucleotide substitution events, short insertions and deletions, gene loss, horizontal transfers, and sequencing errors (for more details, see Lees et al. 2018). JolyTree inferred the tree represented in Fig. 3b with sketch size \(s\) = 500,000 and k-mer size \(k\) = 19 (\(q\) = 0.00001). As every pairwise Mash dissimilarity was < 0.1, the F81 correction was not used. Observed running times were 59, 64, 73, 148, and 391 seconds with 16, 12, 8, 6, and 4 threads, respectively, on an Intel Xeon E5-1660 v4 (16Gb RAM) under Linux Debian 4.9.110-3+deb9u6.

a
b
Figure 3.

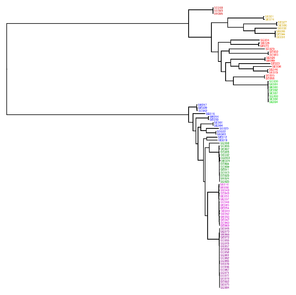
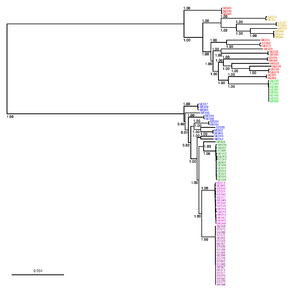
Model tree used for genome data simulation by Lees et al. (2018), and inferred tree obtained with JolyTree. Leaf names are colored according to Lees et al. (2018).

a: Model tree as inferred by Kremer et al. (2016) from Listeria genomes.  
b: Inferred tree with branch support (rate of elementary quartets) represented only at each branch of length > 0.00005; scale bar refers to 0.004 nucleotide substitutions per character.  

To measure the overall phylogenetic signal induced by the estimated distances, the Arboricity coefficient (arb; Guénoche and Garreta 2001) was computed, as well as the mean value \(\overline{\delta}\) related to the \(\delta\) plot approach (Holland et al. 2002). Both coefficients allow the overall treelikeness of a set of pairwise evolutionary distances to be assessed by validating whether each taxon quartet verifies the four-point condition (Zaretskii 1965, Buneman 1971). Treelike distances are assessed by arb close to 1 (e.g. arb > 0.8) and \( \overline{\delta}\) close to 0 (e.g. \(\overline{\delta}\) < 0.2). The dataset simulated by Lees et al. (2018) led to arb = 0.9791 and \(\overline{\delta}\) = 0.0400, therefore assessing that the estimated distances accurately recover the phylogenetic signal induced by the genome sequences. In consequence, both the model and inferred trees are broadly similar (Fig. 3). All internal branches of length > 0.00005 (44% of the 93 internal branches) are correctly reconstructed (Fig. 3b), most of them being validated by branch supports of 1.00 (only three are not associated to the maximum branch confidence value, but they remain well-supported, i.e. 0.90, 0.82, 0.81; see Fig. 3b). The other internal branches (i.e. branch length < 0.00005) are moderately supported (e.g. 60% are associated to branch support < 1.00). When compared to the model tree (Fig. 3a), the inferred tree allows nine incorrectly reconstructed internal branches to be observed (i.e. 9 / 93 = 9.67% of false branches), each being very short (e.g. < 5.10-6). However, the best result reached by Lees et al. (2018) from the same data was a Maximum Likelihood (ML) phylogenetic tree with six incorrectly reconstructed branches (6 / 93 = 6.45%, each being very short too). JolyTree is thus able to quickly infer trees that are comparable to the ones reconstructed by efficient but slower methods. Of note, this simulation result points out that JolyTree is sometimes not able to accurately reconstruct some very short internal branches. This limitation could be explained by the use of the Mash dissimilarity computed by formula \((1)\) that is based on k-mer subsets. Indeed, the sketch size \(s\) could be not large enough to estimate a pairwise dissimilarity from very similar genome sequences with sufficient precision. However, alternative methods based on multiple sequence alignments can be used to quickly infer trees from very closely related genome sequences (e.g. Treangen et al. 2014).

Real-case analyses

To observe the ability of JolyTree to quickly infer accurate species trees from real data, genome assemblies from the RefSeq collection (O'Leary et al. 2015) were considered. For each genus, available assemblies were gathered when their number was between 30 and 300, leading to 187 genome sequence sets (bacteria: 180; archaea: 6; fungi: 1) of varying size (e.g. \(\overline{n}\) = 76 and \(\overline{g}\) = 4.1 Mb). Each dataset was next analyzed by JolyTree (default options) to infer a phylogenetic tree representing the evolutionary relationships within the corresponding genus. All inferred trees are available in Suppl. material 1 together with several descriptive statistics (genome numbers and sizes, GC contents, maximum dissimilarities and distances, treelikeness coefficients, mean branch supports). The 14,244 corresponding genome assemblies are described in Suppl. material 2.

This representative collection of genome sequence sets shows that the GC content is very heterogeneous across genera (Suppl. material 1), i.e. varying from 26.39% (Streptobacillus) to 72.90% (Clavibacter). Within each genus, the GC content is sometimes variable, with the standard deviation of %GC going up to 8.14 (Desulfovibrio). This clearly justifies the use of the F81 correction formula \((3)\) proposed by Tamura and Kumar (2002) to estimate the pairwise evolutionary distances from genome sequences that are often compositionally heterogeneous. The treelikeness of the estimated distances are quite high (e.g. 121 of the 187 genera leads to arb > 0.8 and \(\overline{\delta}\) < 0.2; Suppl. material 1), as well as the number of inferred external non-negative branches (e.g. no negative branch for 113 of the 189 datasets; Suppl. material 1), therefore showing that JolyTree is often able to catch the phylogenetic signal induced by many real genome datasets. Of note, an important number of inferred internal branches are well-supported (e.g. 140 datasets allows observing rates of elementary quartets larger than 0.70 on average; (Suppl. material 1), therefore showing that FastME is able to infer robust phylogenetic trees from the evolutionary distance matrices built from the different genome datasets.

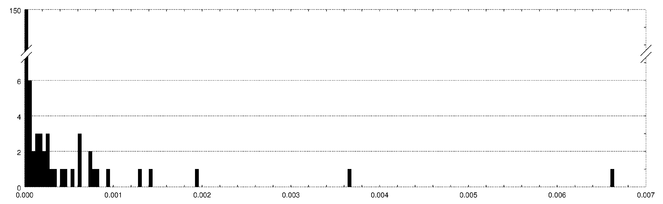
It should be stressed that the data noising strategy had a moderate usefulness on these datasets, as no better tree (according to the BME criterion) than the one inferred by FastME alone was obtained for 125 datasets. This could be explained by the overall good treelikeness of the estimated evolutionary distances (Suppl. material 1), which likely involves few local optima. However, this step remains important in order to assess that an inferred tree is the BME one. Let \(T_0\) be the tree inferred by FastME alone, and \(T\) the one inferred by JolyTree via the data noising strategy. The Fig. 4 represents the distribution of the different values \((\ell(T_0)-\ell(T))/\ell(T_0)\). Among the 62 datasets for which FastME was trapped in a local optimum, Fig. 4 shows a quite moderate improvement for many of them (e.g. less than 0.1% improvement of the BME tree optimality criterion for 57 datasets). However, Fig. 4 also shows that in some cases, the data noising strategy implemented by JolyTree allows observing up to 0.66% tree length improvement, i.e. from \(\ell(T_0)\) = 1.7324 to \( \ell(T)\) = 1.7210 (Megasphaera). The BME tree search approach used by JolyTree can therefore be useful for inferring accurate phylogenetic trees, especially when the overall treelikeness is weak. Of note, as the FastME program runs fast, the data noising strategy does not require important running times, especially when compared with the ones required for estimating all pairwise Mash dissimilarities.

Figure 4.  

Distribution of the normalized Balanced Minimum Evolution (BME) tree length differences observed between phylogenetic trees inferred by FastME with and without the data noising strategy implemented by JolyTree. This distribution represents 187 observed values \(\Delta(T_0, T) = (\ell(T_0)-\ell(T))/\ell(T_0)\), where \(T_0\) is the tree inferred by FastME alone, \(T\) the one inferred by JolyTree via the data noising strategy, and \(\ell(T)\) the BME tree length estimate of \(T\). A tree \(T\) is considered as more accurate that \(T_0\) when \(\Delta(T_0, T)\) > 0.

Thanks to its ability to run on multiple threads, JolyTree is quite fast. On an Intel Xeon E5-1660 v4 (16Gb RAM) running under Linux Debian 4.9.110-3+deb9u6, 90% of the 187 genome datasets were analyzed in less than 15 and 5 minutes each, on 6 and 12 threads, respectively. The main variable having a negative impact on the overall running times is the number \( n\) of genomes, e.g. with quite comparable genome sizes (e.g. \(\overline{g}\) = 6.5 Mb), observed running times varied from 69 and 46 seconds with \(n\) = 30 (Duganella) to 30 and 19 minutes with \(n\) = 291 (Rhizobium) on 6 and 12 threads, respectively. Average genome size \(\overline{g}\) has less impact on the overall running times, as it only slows the Mash sketching step, e.g. with \(n\) = 34, observed running times varied from 62 and 16 seconds with \(\overline{g}\) = 2.8 Mb (Caldicellulosiruptor) to 4 and 3 minutes with \(\overline{g}\) = 34.1 Mb (Aspergillus) on 6 and 12 threads, respectively. JolyTree therefore represents a useful tool to quickly infer phylogenetic trees from large sets of genome sequences on standard computers.

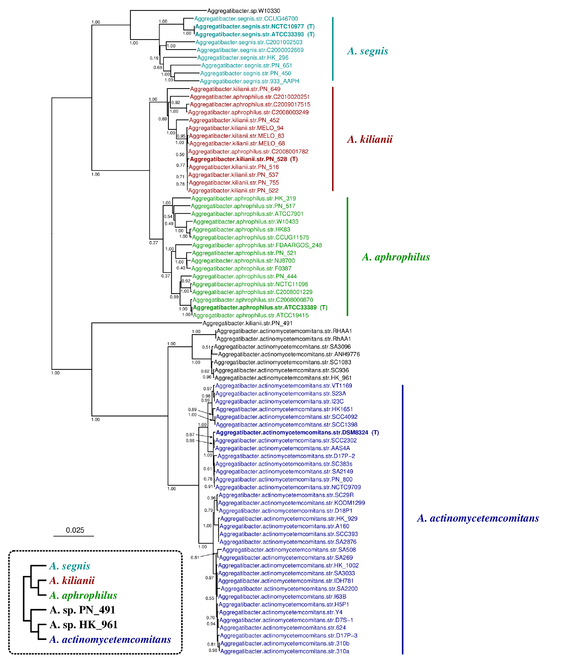
Finally, to illustrate the accuracy of the phylogenetic trees inferred by JolyTree, a bibliographical survey was performed for each of the 187 genera to find recently published phylogenetic trees for comparison. Considering only genome datasets made up by at least four species, as well as only robust phylogenomics analyses based on core genome data for comparison, this survey led to six genera: Aggregatibacter (Murra et al. 2018), Borreliella (Casjens et al. 2018), Elizabethkingia (Nicholson et al. 2017, Perrin et al. 2017), Lactococcus (Yu et al. 2017), Providencia (Galac and Lazzaro 2012), and Ralstonia (Zhang and Qiu 2015).

The Aggregatibacter tree inferred by JolyTree (Fig. 5) is very similar to the model tree of Murra et al. (2018). Indeed, both trees recover the same phylogenetic relationships among the four species A. actinomycetemcomitans, A. aphrophilus, A. kilianii, and A. segnis, all being assessed by the maximum branch support value (Fig. 5). However, it should be stressed that some strains labelled A. actinomycetemcomitans do not likely belong to this species (i.e. strains ANH9776, HK_961, RHAA1, RhAA1, SA3096, SC936, and SC1083) as the estimated distance between each of these genomes and the type strain genome (DSM8324) is larger than 0.05 (e.g. from 0.0568 to 0.0620). Indeed, as the evolutionary distance \(d_{ij}\) estimated by JolyTree between two genomes \(i\) and \( j\) is very similar to the one-complement \( a_{ij}\) of the Average Nucleotide Identity (ANI), especially when \( d_{ij}\) < 0.1 (see above), it is expected that \( i\) and \( j\) do not belong to the same species when \( d_{ij} \approx a_{ij}\) > 0.05, which is the recommended cut-off for species delineation (e.g. Goris et al. 2007, Topaz et al. 2018). Following the same rationale, the phylogenetic tree in Fig. 5 also shows that each strain PN_491 and W10330 likely belongs to a putative new Aggregatibacter species.

Figure 5.  

Phylogenetic tree inferred by JolyTree from the RefSeq genomes belonging to the genus Aggregatibacter. For each type strain (in bold), the clade determined by the isolates expected to belong to the same species (e.g. estimated pairwise distances < 0.05) is labeled by the species name and colored accordingly. Leaf names were automatically generated. Scale bar corresponds to an estimated evolutionary distance of 0.025. The inset summarizes a model tree of the Aggregatibacter species based on the phylogenetic analysis of Murra et al. (2018).

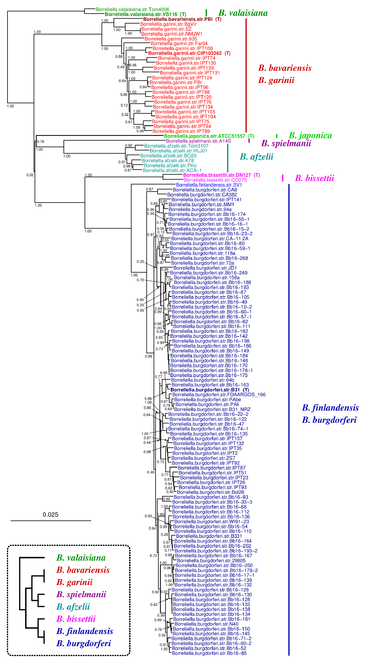
The Borreliella tree inferred by JolyTree is represented in Fig. 6, together with a model tree topology summarizing the phylogenetic relationships among species based on the phylogenomics analysis of Casjens et al. 2018. The only difference is the clade B. afzelli + B. spielmanii that groups with the clade B. bisettii + B. burgdorferi + B. finlandensis but not with B. bavariensis + B.garinii (Fig. 6). This conflicting grouping is likely caused by a long branch attraction between B. japonica and B. spielmanii, as a species tree similar to the model tree (Casjens et al. 2018) is inferred by JolyTree when removing these two genomes (not shown). A more accurate phylogenetic tree is therefore expected when more B. japonica and B. spielmanii genomes are available in the RefSeq collection. However, when considering the present genome dataset, the likely incorrect clade B. afzelli + B. bisettii + B. burgdorferi + B. finlandensis + B. japonica + B. spielmanii could be easily detected as its corresponding internal branch is weakly supported by a rate of elementary quartets of 0.32 (Fig. 6).

Figure 6.  

Phylogenetic tree inferred by JolyTree from the RefSeq genomes belonging to the genus Borreliella. For each type strain (in bold), the clade determined by the isolates expected to belong to the same species (e.g. estimated pairwise distances < 0.05) is labeled by the species name and colored accordingly. Leaf names were automatically generated. Scale bar corresponds to an estimated evolutionary distance of 0.025. 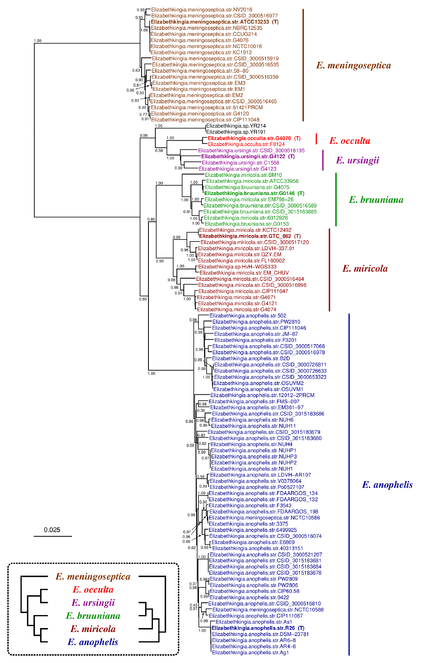The inset summarizes a model tree of the Borreliella species based on the phylogenetic analysis of Casjens et al. (2018). The two genomes B. finlandensis and B. spielmanii, as well as the clade B. afzelii are highlighted to be comparable with the phylogenetic analysis of Casjens et al. (2018).

Concerning the genus Elizabethkingia, two recently published conflicting phylogenetic trees exist (inset in Fig. 7). Rooted with the clade E. meningoseptica, the first tree is of the form \(\small (((E.bruuniana,E.ursingii),E.miricola),E.anophelis)\)  (see doi:10.6084/m9.figshare.4585492.v1 from Perrin et al. (2017), whereas the second tree is of the form \(\small ((E.occulta,E.ursingii),(E.bruuniana,(E.miricola,E.anophelis)))\) (Nicholson et al. 2017). Both phylogenetic trees were inferred by ML from large multi-gene datasets and every species clade is assessed by maximum support values (Nicholson et al. 2017, Perrin et al. 2017). Interestingly, the tree reconstructed by JolyTree from the Elizabethkingia genome dataset (Fig. 7) leads to the diagrammatic species tree \(\small ((E.occulta,E.ursingii),((E.bruuniana,E.miricola),E.anophelis))\). Agreeing with Nicholson et al. (2017), the clade E. occulta + E. ursingii is strongly supported (i.e. rate of elementary quartets = 0.98). However, contrary to Nicholson et al. (2017), the clade E. bruuniana + E. miricola is well supported too (i.e. rate of elementary quartets = 0.80), whereas the clade E. anophelis + E. bruuniana + E. miricola is quite less supported (0.65). The phylogenetic tree inferred by JolyTree therefore hilghlights some weakness of the phylogenetic signal induced by the Elizabethkingia dataset, and questions the accuracy of the two model trees inferred by Nicholson et al. (2017) and Perrin et al. (2017). Of note, the phylogenetic tree in Fig. 7 also shows that the two strains YR191 and YR214 are identical and belong to a new Elizabethkingia species.

Figure 7.  

Phylogenetic tree inferred by JolyTree from the RefSeq genomes belonging to the genus Elizabethkingia. For each type strain (in bold), the clade determined by the isolates expected to belong to the same species (e.g. estimated pairwise distances < 0.05) is labeled by the species name and colored accordingly. Leaf names were automatically generated. Scale bar corresponds to an estimated evolutionary distance of 0.025. The inset summarizes two model trees of the Elizabethkingia species based on the phylogenetic analyses of Nicholson et al. (2017) and Perrin et al. (2017) (left and right topology, respectively).

The Lactococcus tree inferred by JolyTree (Fig. 8) represents the same phylogenetic relationships among species than the model tree inferred by Yu et al. (2017). It clearly shows that L. lactis is in fact separated into two species: one associated with the type strain L. lactis subsp. cremonis ATCC 19257, and the other with the type strain L. lactis subsp. lactis ATCC 19435. It also allows many incorrectly named L. garvieae strains to be observed, some belonging to the species L. petauri, and others to new undefined species (i.e. strains A1, DCC43, I113, and 122061).

Figure 8.  

Phylogenetic tree inferred by JolyTree from the RefSeq genomes belonging to the genus Lactococcus. For each type strain (in bold), the clade determined by the isolates expected to belong to the same species (e.g. estimated pairwise distances < 0.05) is labeled by the species name and colored accordingly. Leaf names were automatically generated. Scale bar corresponds to an estimated evolutionary distance of 0.025. The inset summarizes a model tree of the Lactococcus species based on the phylogenetic analysis of Yu et al. (2017).

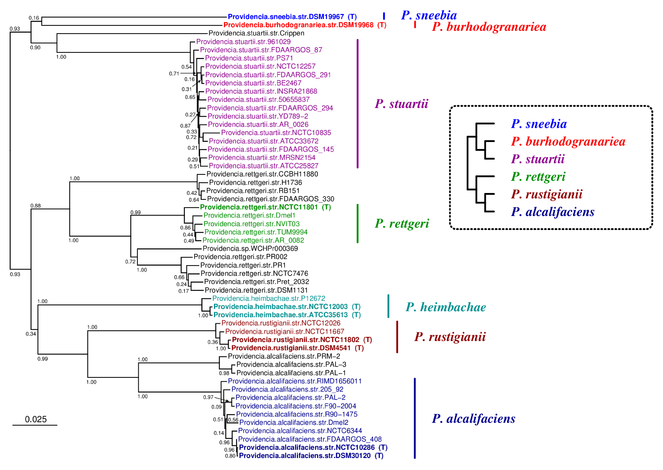
The Providencia tree inferred by JolyTree is represented in Fig. 9, together with a model tree topology summarizing the phylogenetic relationships among species inferred by Galac and Lazzaro (2012). Both species trees are quite similar, with every species clade being strongly supported. The only difference is the grouping of P. burhodogranariea and P. sneebia into one clade, which is likely caused by a long branch attraction due to a low genome sampling for both species and identifiable by a low branch support of 0.16 (see a similar case in the Borreliella tree above). Of note, the tree in Fig. 9 allows observing that many new species need to be described within the genus Providencia.

Figure 9.  

Phylogenetic tree inferred by JolyTree from the RefSeq genomes belonging to the genus Providencia. For each type strain (in bold), the clade determined by the isolates expected to belong to the same species (e.g. estimated pairwise distances < 0.05) is labeled by the species name and colored accordingly. Leaf names were automatically generated. Scale bar corresponds to an estimated evolutionary distance of 0.025. 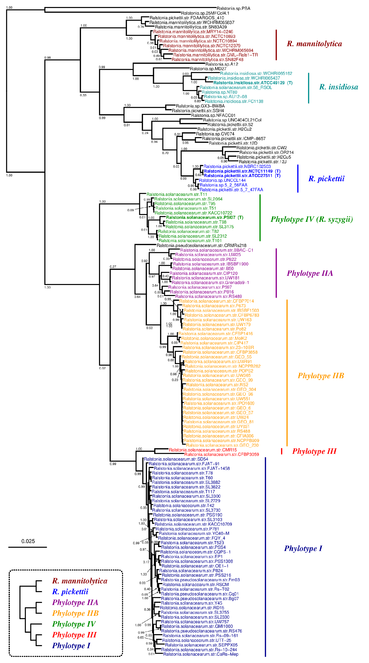The inset summarizes a model tree of the Providencia species based on the phylogenetic analysis of Galac and Lazzaro (2012). The clade P. stuartii is highlighted to be comparable with the tree of Galac and Lazzaro (2012).

The phylogenetic relationships among Ralstonia species was deeply studied by Zhang and Qiu (2015) and is summarized in Fig. 10. Based on a ML analysis of a large core-gene set, Zhang and Qiu (2015) determined that R. solanacearum species complex distributes into five phylotypes. As shown in Fig. 10, the Ralstonia tree inferred by JolyTree allows observing the same phylogenetic relationships among species, with the only exception of the Phylotype IV clade that is first emerging within the R. solanacearum species complex in the tree reconstructed by JolyTree. However, this likely incorrect branching is identifiable by a very low support value (i.e. 0.02; see Fig. 10). In complement, this tree shows that many strains are incorrectly named R. mannitolilytica or R. pickettii, therefore requiring new species proposals within this genus.

Figure 10.  

Phylogenetic tree inferred by JolyTree from the RefSeq genomes belonging to the genus Ralstonia. For each type strain (in bold), the clade determined by the isolates expected to belong to the same species (e.g. estimated pairwise distances < 0.05) is labeled by the species name and colored accordingly. Leaf names were automatically generated. Scale bar corresponds to an estimated evolutionary distance of 0.025. The inset summarizes a model tree of the Ralstonia species based on the phylogenetic analysis of Zhang and Qiu (2015). The clade R. mannitolytica, as well as the five clades Phylotype I, IIA, IIB, III and IV are highlighted to be comparable with the phylogenetic analysis of Zhang and Qiu (2015).

These detailed phylogenetic analyses of the six genera Aggregatibacter, Borreliella, Elizabethkingia, Lactococcus, Providencia and Ralstonia show that JolyTree is a useful tool to quickly infer species trees from whole genome assemblies that are comparable with trees reconstructed from the concatenation of large sets of multiple homologous sequence alignments. They also show that these phylogenetic trees are practical representations to detect new species within a bacterial genus.

Conclusions

This paper describes a novel bioinformatics procedure, implemented by the Bash script JolyTree (gitlab.pasteur.fr/GIPhy/JolyTree), to perform a complete phylogenetic analysis from unaligned genome sequence sets. Such procedure is quite fast because it takes advantage of the ability of the pairwise distance estimate step to be run on multiple threads. Simulation and real case analyses have shown that JolyTree leads to accurate trees. Some incorrect branching can be observed within the inferred phylogenetic trees, but they are often assessed by weak branch supports. Therefore, JolyTree represents a useful approach for performing phylogenetic analyses with fast running times from hundreds of genome assemblies. Of note, this bioinformatics procedure was used previously for inferring Corynebacterium (Dazas et al. 2018), Mucor circinelloides (Garcia-Hermoso et al. 2018) and Escherichia coli (Nadimpalli et al. 2019) trees.

More generally, this paper confirms the usefulness of the MinHash dissimilarity and its ability to efficiently approximate the pairwise p-distance (and the related ANI similarity) between two genome contig sets. However, this paper highlights the importance of transforming a p-distance value into an evolutionary distance estimate in the context of phylogenetic inference, especially when p-distance values are large (e.g. > 0.1). The use of the F81-transformation represents a very simple but efficient way to quickly obtain efficient pairwise evolutionary distance estimates. Of note, such transformation can be easily adaptated with future implementations of the pairwise Mash dissimilarities (e.g. Zhao 2018, Baker and Langmead 2018).

Acknowledgements

This manuscript is dedicated to the memory of Nicolas Joly, who helped to improve the implementation of the script JolyTree for running on multiple threads. The author thanks Laetitia Fabre, Julien Guglielmini and Rachel Legendre for useful comments on the manuscript. The author is also grateful to Brian D. Ondov for reviewing this manuscript. The author is obliged to Sylvain Brisse and to the Hub de Bioinformatique et Biostatistique, Institut Pasteur, Paris (France), for support.

Author contributions

AC conceived the presented idea, implemented the script, conceived the simulations, performed the computations, and wrote the manuscript.

Conflicts of interest

No conflict of interest to declare.

References

Supplementary materials

Suppl. material 1: Overview of the analysis of 187 genus datasets (bacteria: 180; archaea: 6; fungi: 1) 
Authors:  A. Criscuolo
Data type:  spreadsheet (xlsx format)
Brief description: 

For each genus, the table reports the number of genomes (no. taxa), the mean genome sequence size (mean genome size) and the associated standard deviation (SD genome size), the mean percentage of observed GC content (mean %GC) and the associated standard deviation (SD %GC), the largest estimated Mash dissimilarity (max Mash dissimilarity) and F81-corrected Mash distance (max F81 distance), the treelikeness coefficients (arboricity and mean delta), the proportion of external negative branches (% negative branch), the mean rate of elementary quartets (mean branch support) and the associated standard deviation (SD branch support), and the inferred phylogenetic tree in NEWICK format.


Download file (351.50 kb)
Suppl. material 2: List of the 14,244 genome assemblies used to build the 187 genus datasets 
Authors:  A. Criscuolo
Data type:  zipped tabulation-separated values
Brief description: 

Each raw contains the taxon name used during the JolyTree analysis (column 1), followed by the corresponding entry from the RefSeq assembly report (ftp.ncbi.nlm.nih.gov/genomes/ASSEMBLY_REPORTS/assembly_summary_refseq.txt).


Download file (764.46 kb)
login to comment