The trigonometric parallax is now the most powerful model-independent method for measuring astronomical distances. Astronomical research still needs more independent methods of distance measurements, such as using the phase information of the sources (Zou 2020). In the following, we propose yet another independent method. This method takes into account the fact that the received electromagnetic waves are spherical waves instead of assumed plane waves. It requires that the source is far enough to generate spherical waves like a point source. However, it is difficult to distinguish spherical waves from the plane waves for very distant sources. Only with the latest development of telescope positioning, this straightforward method becomes possible.

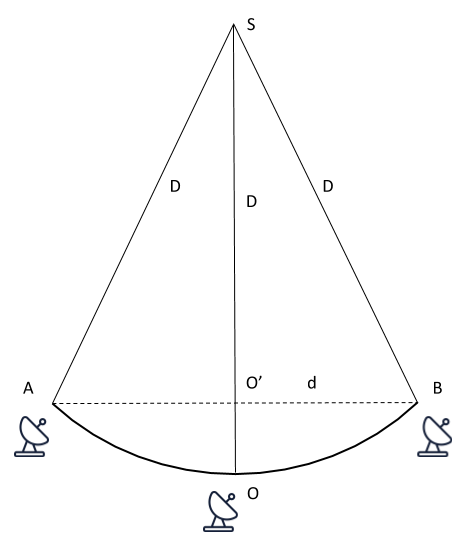
A schematic plot is shown in Fig. 1. An astronomical source emits spherical electromagnetic waves from point S. Three telescopes are settled at positions A, O, and B. The telescopes are placed on a circle by satisfying the center of the circle being at point S. This requirement can be achieved by satisfying that the 3 telescopes are measuring the same wavefront. With the successful settlement, one only needs to measure the distance of OO' (\(b\)) as shown in Fig. 1. The distance is expressed as \(D={d^2 \over 2 b}\), where \(d\) is half of the distance between A and B. With a given distance of an astronomical object in the Milky Way galaxy, for instance \(D = 10^{20} {\rm cm}\), and the distance of two telescopes, \(d=5 \times 10^{8} {\rm cm}\), which is the scale of the VLBI telescopes, the required length should be distinguished is \(b =1.25 \times 10^{-3} {\rm cm}\). The accuracy of the length measurement could be realized in the near future. Considering the current accuracy of VLBI is about 1 mm (Schuh and Behrend 2012), one may expect the farthest distance can be measured is around \(D \sim 10^{18} {\rm cm}\). With the improved position accuracy, as well as the increased baseline, the distances of even further astronomical objects can be directly measured eventually.

Figure 1.  

A schematic figure shows the spherical wave observed with 3 telescopes located at positions A, O, and B. The 3 telescopes are settled at the spherical wavefront. The source S is the center of the circle. With the measuring of distance \(b\)=OO', one is able to get the distance \(D = {d^2 \over 2b}\), where \(d\) is the distance between B and O'.

The schematic configuration is designed for clear expression. An actual observing system does not require the 3 telescopes to be located in the circle. Only the precise positions and accurate time sequences are required. The existing VLBI system might be directly used with this method to measure the distances of nearby objects.

Gravitational waves can also be used to measure the distance of the source in a similar way if the time and the position of the receiver are obtained accurately.

The accuracy is basically restricted by the working wavelength. With THz telescopes, one is able to measure the small distance of \(b \sim {\rm mm}\). Notice that with the increase of the baseline \(d\), the measurable distance \(D\) increases quickly. This might be a potentially powerful tool to measure extra-galactic cosmological distances directly. Considering 3 spaceborne telescopes in the Earth's orbit with \(d \sim 10^{13}cm\) , with the position accuracy of 1 mm, the measurable distance can reach up to 1 Gpc.

The three-telescope system is sensitive to the sources located on the same plane of the system. A more general system could consist of four telescopes, by putting the fourth telescope non-coplanarly.

Research at Perimeter Institute is supported in part by the Government of Canada through the Department of Innovation, Science and Economic Development Canada and by the Province of Ontario through the Ministry of Colleges and Universities. This work was supported by the National Natural Science Foundation of China (Grant No. U1738132 and 11773010).