Scale invariance of intrinsic patterns is an important concept in geology that can be observed in numerous geological objects and phenomena. These geological objects and phenomena are described as containing statistically self-similar patterns often modeled with fractal geometry. Examples include the perimeter of coastlines (Mandelbrot 1983) and oil and gas field distributions (Hein 1999). Fractal geometry has also been used extensively to characterize pore space and fracture distribution of both carbonate and clastic rocks as well as the transport properties of porous media and fluid flow in reservoirs (Pape et al. 1987, Pape et al. 1999). In this short paper we apply the modified Kozeny-Carman equation to estimate permeability from fractal properties of moldic pore spaces. The Kozeny-Carman equation describes the relationship between permeability and porosity assuming laminar flow in tubular cylinders. The tubular cylinders constitute the pigeon hole fractal model and are a particularly useful approximation of moldic pores in three dimensions. We apply the equation to data from the Happy Spraberry Field, in Garza County, Texas.

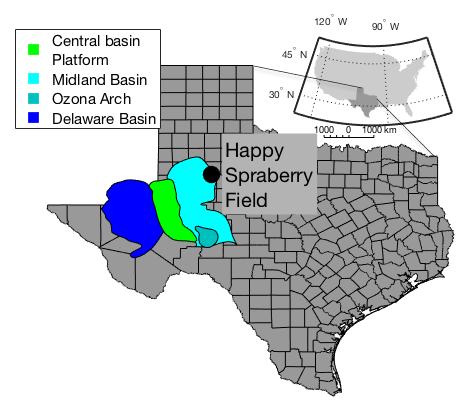
The Happy Spraberry Field Texas is located in Garza County on the northern part of the Midland Basin (Fig. 1). It produces oil from heterogeneous shallow-shelf carbonates of the Permian-aged Lower Clear Fork Formation. Core samples obtained from the field indicate the reservoir facies contain oolitic skeletal grainstones/packstones and skeletal rudstones. The reservoir facies have cemented and dissolution-enhanced pore types caused by facies selective diagenesis. Moldic pores are the most abundant across the field and dominate the oolitic skeletal grainstone packstone facies.

Figure 1.  

Map showing the location of the Happy Spraberry Field in Garza County, Texas.

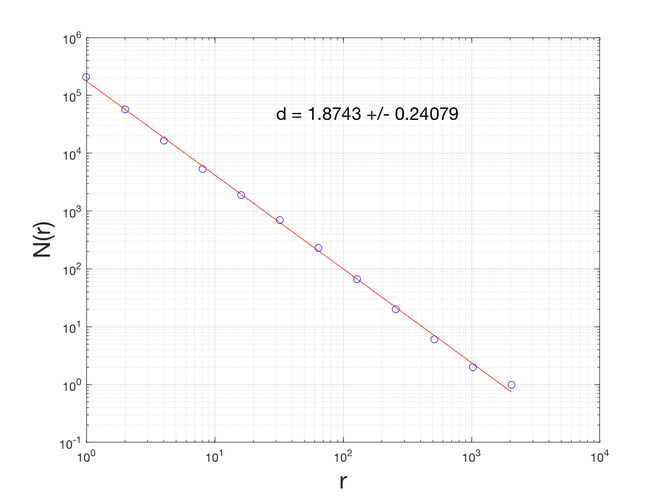
We make use of thin section photomicrographs of the reservoir facies from a well in the Happy Spraberry Field. We use a newly developed program to interactively model the pore paces as tubular cylinders and apply the box-counting method to extract the porosity and the Minkowski-Bouligand fractal dimension (For more geoscience programs, see Amosu and Sun (2017a), Amosu and Sun (2017b), Amosu and Sun (2018)). For a pigeonhole fractal model Pape et al. (1987) and Pape et al. (1999) derived equations that relate tortuosity and porosity with the fractal dimension. The first equation shows the modified Kozeny-Carman equation. The second and third equation relates tortuosity and porosity to the fractal dimension; the equation is only valid for fractal dimensions with values between 2 and 3.

\(k={ \phi \over {8T}} r_{eff}^2 \)

\(T= {1.34 \left ({r_{grain} \over r_{eff} } \right)^ {0.67(D-2)}} \)

\(\phi= {0.5 \left ({r_{grain} \over r_{eff} } \right)^ {0.39(D-3)}} \)

In the above equations, T is tortuosity, r_grain is average grain size, r_eff is the effective pore radius, D is the fractal dimension, k is permeability and ø is porosity.

Fig. 2 shows the pigeonhole model used to approximate the moldic pores. Fig. 3 depicts how the fractal dimension is estimated. Plausible values of the fractal dimension range from 1.63 to 2.11, hence equation (2) is applicable for values greater than 2. We choose the representative value of 2.11 and substitute it in the second and third equations to obtain:

Figure 2.  

Figure showing the application of the pigeonhole fractal model to the pore spaces in the thin-section photomicrograph.

Figure 3.  

Figure depicting how the fractal dimension is estimated using the box-counting method.

\(T= {1.34 \left ({r_{grain} \over r_{eff} } \right)^ {0.07}} \)

\(\phi = {0.5 \left ({r_{grain} \over r_{eff} } \right)^ {-0.35}} \)

Combining these two two equations with the first equation, we obtain:

\(k ={4.3 *10^{11} r_{grain}^2 \phi^{7/5}}\)

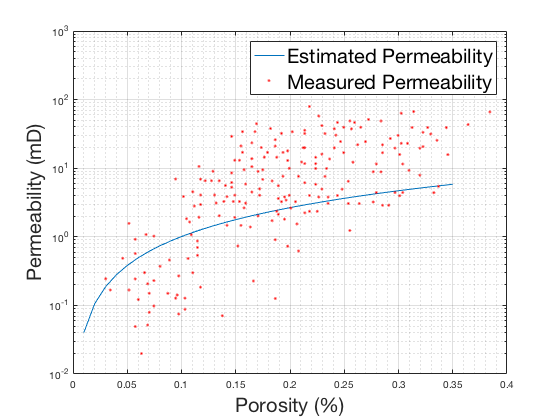
Using an average value of grain size radius = 250000 nm and porosity ranging from 0 to 35%, we compare the estimated permeabilities to laboratory-measured core permeabilities from the field. Fig. 4 shows the estimated permeability-porosity relationship has a good match with laboratory-measured permeability-porosity relationship especially for porosity values less than 20%.

Figure 4.  

Figure depicting the porosity-permeability relationship.

The pigeonhole fractal is used to successfully characterize the moldic pores in the reservoir facies of carbonate rocks and extract the fractal dimension. We then apply the Kozeny-Carman equation and equations relating the tortuosity and the porosity to the fractal dimension to establish an empirical relationship between permeability and porosity.